Fungsi Surjektif

Fungsi Surjektif. Dengan kata lain seluruh elemen b merupakan jelajah dari f. Contoh soal fungsi surjektif injektif dan bijektif lengkap dengan beserta jawaban soal 1 tentang fungsi surjektif lihat keempat diagram panah dibawah ini yang merupakan fungsi surjektif adalah. Fungsi f merupakan fungsi yang surjektif. Fungsi f disebut fungsi pada (onto) atau surjektif jika setiap ypada b memiliki preimage.

Tentukan mana fungsi surjektif, injektif, dan bijektif From brainly.co.id

Souqy jelas sakit lirik Tabel angsuran kpr bank mandiri Teknik proyeksi bisnis Template label nama

Click sifat fungsi injektif.pdf link to view the file. ℝ → ℝ yang didefinisikan sebagai g(x) = x 2. Perhatikan gambar di bawah untuk menambah pemahaman sobat idschool. Fungsi surjektif biasanya dipenuhi apabila jumlah anggota kodomain sama atau lebih sedikit dari anggota domain. Click sifat fungsi surjektif.pdf link to view the file. Fungsi f dikatakan surjektif (surjective) atau pada (onto) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a.

Fungsi f disebut fungsi pada (onto) atau surjektif jika setiap ypada b memiliki preimage.

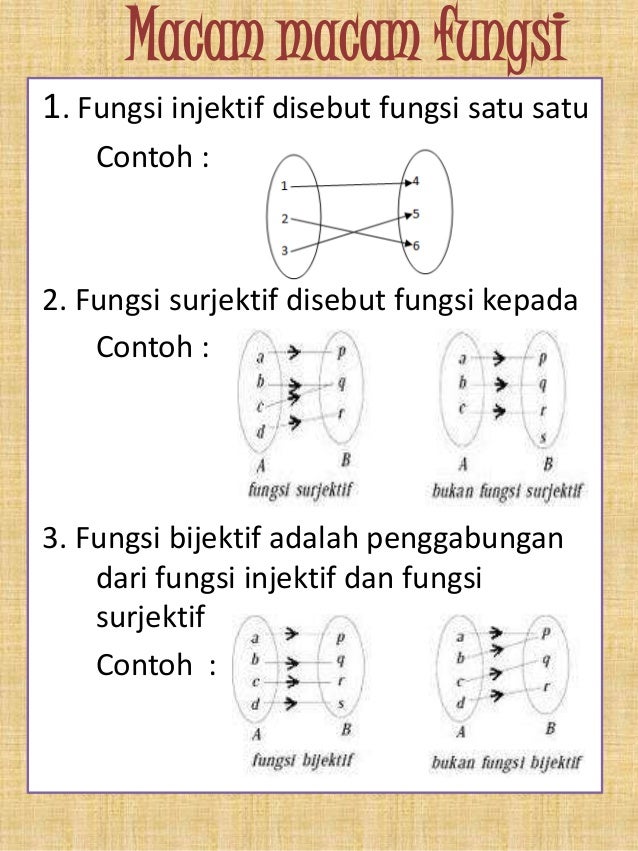
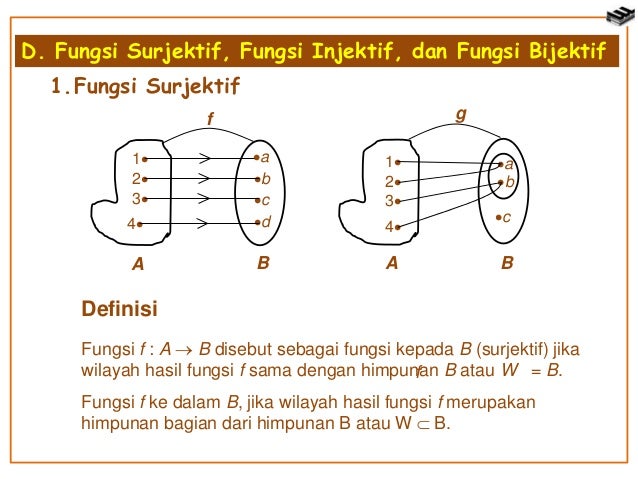
Contoh soal fungsi surjektif injektif dan bijektif lengkap dengan beserta jawaban soal 1 tentang fungsi surjektif lihat keempat diagram panah dibawah ini yang merupakan fungsi surjektif adalah. Karena f injektif dan surjektif, f merupakan suatu bijeksi. Fungsi surjektif (onto) a b a b pada tidak pada fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a. 𝐴 → 𝐵 yang didefinisikan dengan diagram panah adalah suatu fungsi yang surjektif karena daerah hasil 𝑓 adalah sama dengan kodomain dari 𝑓 (himpunan b). Dilansir dari cuemath, fungsi surjektif adalah fungsi daerah hasilnya (range) sama dengan kodomainnya. About press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features press copyright contact us creators.

Source: barucontohsoal.blogspot.com

Jawab misal 𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 dan 𝐵 = {𝑥, 𝑦, 𝑧} dan fungsi 𝑓: ℝ → ℝ yang didefinisikan sebagai g(x) = x 2. Jawab misal 𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 dan 𝐵 = {𝑥, 𝑦, 𝑧} dan fungsi 𝑓: Fungsi surjektif, bijektif, dan injektif. Jadi, f merupakan fungsi surjektif.

Source: kimiamath.com

A → b disebut fungsi surjektif, jika setiap elemen di b mempunyai pasangan di a atau w f = b. A → b di mana f = {(1, a), (2, b), (3, c), (4, c)} ℝ → ℝ yang didefinisikan sebagai g(x) = x 2. Jadi bila kita dapat membuktikan kebenaran kuantor berikut: Fungsi surjektif (onto) a b a b pada tidak pada fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a.

Source: kimiamath.com

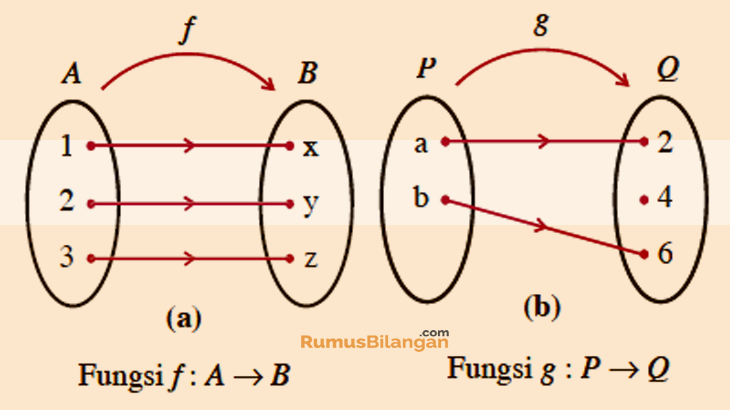
Namun, bila ada y∈ b sehingga setiap x∈a, f (x)≠ y. Dengan kata lain seluruh elemen b merupakan jelajah dari f. Jawab misal 𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 dan 𝐵 = {𝑥, 𝑦, 𝑧} dan fungsi 𝑓: Fungsi surjektif fungsi surjektif merupakan fungsi yang daerahnya merupakan hasil dari sekelompok teman, yang artinya setiap anggota di daerah teman, mempunyai pasangan dengan anggota himpunan daerah asal (sepasang anggota himpunan asli dengan daeran kawan boleh bersamaan). Berikut beberapa contoh relasi fungsi surjektif dalam digaram pemetaan relasi fungsi.

Source: tipsbelajarcarapintar.blogspot.com

\ a \rightarrow b$ dikatakan surjektif (atau memetakan a pada b) bila f(a)=b yang berarti range f adalah semua anggota himpunan b sehingga secara ekivalen $f: ∀y∈ b ∃x∈ a sehingga y = f (x) maka f surjektif. Untuk memahami konsep fungsi tujuan, pertimbangkan himpunan a = {1, 2, 3, 4} dan himpunan b = {a, b, c}. Fungsi surjektif juga sering disebut sebagai fungsi onto. Namun, bila ada y∈ b sehingga setiap x∈a, f (x)≠ y.

Source: raafitrizone.blogspot.com

Fungsi f dikatakan injektif jika dan hanya jika untuk setiap x, y a dengan f(x) = f(y) berlaku x = y. Dengan kata lain seluruh elemen b merupakan jelajah dari f. \ a \rightarrow b$ dikatakan surjektif (atau memetakan a pada b) bila f(a)=b yang berarti range f adalah semua anggota himpunan b sehingga secara ekivalen $f: Fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a. Sifat fungsi surjektif atau pada atau onto previous activity sifat fungsi :

Source: brainly.co.id

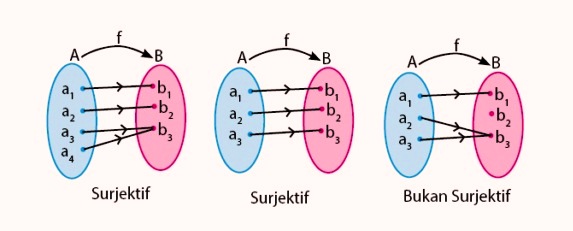
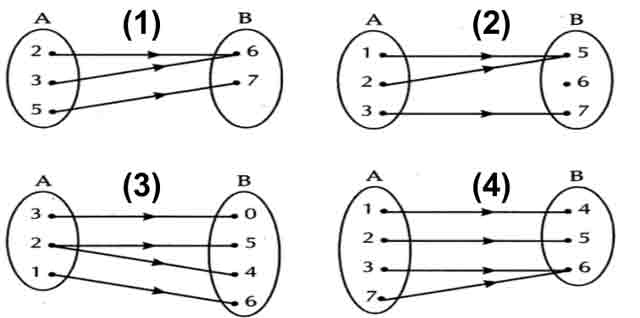
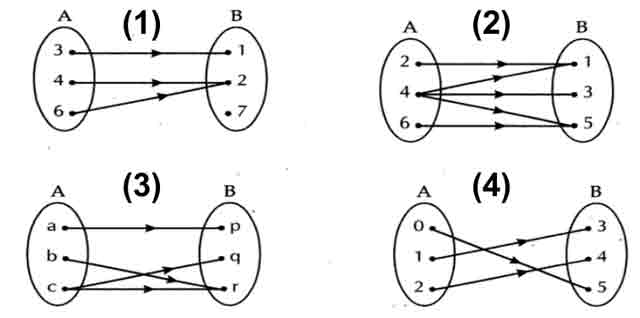
Berdasarkan konsep ini, maka dapat disimpulkan bahwa gambar diagram panah yang menunjukkan fungsi surjektif adalah gambar (1) dan (4). Dengan kata lain seluruh elemen b merupakan jelajah dari f. Jadi maksudnya jumlah anggota daerah asal ≥ jumlah anggota daerah. A → b dikatakan kepada atau surjektif jika setiap y ∈ b terdapat x ∈a sehingga y = f (x), yaitu semua anggota b habis terpasang dengan anggota a. Jawab misal 𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 dan 𝐵 = {𝑥, 𝑦, 𝑧} dan fungsi 𝑓:

Source: rumuspelajaran.com

Jadi bila kita dapat membuktikan kebenaran kuantor berikut: Fungsi f disebut fungsi pada himpunan b. Bukan fungsi surjektif, karena tidak semua bilangan termasuk daerah kawan. Jadi bila kita dapat membuktikan kebenaran kuantor berikut: \ a \rightarrow b$ dikatakan surjektif (atau memetakan a pada b) bila f(a)=b yang berarti range f adalah semua anggota himpunan b sehingga secara ekivalen $f:

Source: contohsoalku.co

Dengan kata lain seluruh elemen b merupakan jelajah dari f. Fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a. A → b di mana f = { (1, a), (2, b), (3, c), (4, c)} Fungsi f disebut fungsi pada (onto) atau surjektif jika setiap ypada b memiliki preimage. Fungsi f dikatakan injektif jika dan hanya jika untuk setiap x, y a dengan f(x) = f(y) berlaku x = y.

Source: br1monline.blogspot.com

Berdasarkan konsep ini, maka dapat disimpulkan bahwa gambar diagram panah yang menunjukkan fungsi surjektif adalah gambar (1) dan (4). A → b di mana f = { (1, a), (2, b), (3, c), (4, c)} Dengan demikian, apakah fungsi berikut ini merupakan fungsi injektif, surjektif atau bijektif adalah paparan yang telah dijelaskan di atas. Misalnya suatu fungsi himpunan a→b, maka setiap elemen dari b memiliki relasi dengan elemen a tanpa ada satupun elemen di b yang tidak berpasangan. \ a \rightarrow b$ dikatakan surjektif (atau memetakan a pada b) bila f(a)=b yang berarti range f adalah semua anggota himpunan b sehingga secara ekivalen $f:

Source: rumusbilangan.com

Fungsi surjektif juga sering disebut sebagai fungsi onto. Ada tiga sifat fungsi yang dibahas, dalam file ini dibahas sifat injektif previous activity sifat fungsi : Untuk memahami konsep fungsi tujuan, pertimbangkan himpunan a = {1, 2, 3, 4} dan himpunan b = {a, b, c}. Fungsi surjektif, bijektif, dan injektif. Bukan fungsi surjektif, karena tidak semua bilangan termasuk daerah kawan.

Source: blogmipa-matematika.blogspot.com

Dengan demikian, apakah fungsi berikut ini merupakan fungsi injektif, surjektif atau bijektif adalah paparan yang telah dijelaskan di atas. Fungsi f disebut fungsi pada himpunan b. Fungsi surjektif (onto) a b a b pada tidak pada fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a. Untuk memahami konsep fungsi tujuan, pertimbangkan himpunan a = {1, 2, 3, 4} dan himpunan b = {a, b, c}. Bukan fungsi bijektif, karena unsur fungsi injektif tidak terpenuhi.

Source: blogmipa-matematika.blogspot.com

A → b dikatakan kepada atau surjektif jika setiap y ∈ b terdapat x ∈a sehingga y = f (x), yaitu semua anggota b habis terpasang dengan anggota a. Click sifat fungsi surjektif.pdf link to view the file. ℝ → ℝ yang didefinisikan sebagai g(x) = x 2. 𝐴 → 𝐵 yang didefinisikan dengan diagram panah adalah suatu fungsi yang surjektif karena daerah hasil 𝑓 adalah sama dengan kodomain dari 𝑓 (himpunan b). A → b di mana f = {(1, a), (2, b), (3, c), (4, c)}

Source: brainly.co.id

Jadi maksudnya jumlah anggota daerah asal ≥ jumlah anggota daerah. Contoh soal fungsi surjektif injektif dan bijektif lengkap dengan beserta jawaban soal 1 tentang fungsi surjektif lihat keempat diagram panah dibawah ini yang merupakan fungsi surjektif adalah. Dengan kata lain seluruh elemen b merupakan jelajah dari f. Dengan kata lain seluruh elemen b merupakan jelajah dari f. Satu elemen b dapat berpasangan.

Source: kitabelajar.github.io

Fungsi f disebut fungsi pada (onto) atau surjektif jika setiap ypada b memiliki preimage. Karena f injektif dan surjektif, f merupakan suatu bijeksi. Jadi bila kita dapat membuktikan kebenaran kuantor berikut: Berdasarkan konsep ini, maka dapat disimpulkan bahwa gambar diagram panah yang menunjukkan fungsi surjektif adalah gambar (1) dan (4). Jadi, f merupakan fungsi surjektif.

Source: bagikancontoh.blogspot.com

Dengan demikian, apakah fungsi berikut ini merupakan fungsi injektif, surjektif atau bijektif adalah paparan yang telah dijelaskan di atas. Dengan kata lain seluruh elemen b merupakan jelajah dari f. Jadi bila kita dapat membuktikan kebenaran kuantor berikut: Bukan fungsi surjektif, karena tidak semua bilangan termasuk daerah kawan. Satu elemen b dapat berpasangan.

Source: slideshare.net

Untuk memahami konsep fungsi tujuan, pertimbangkan himpunan a = {1, 2, 3, 4} dan himpunan b = {a, b, c}. Fungsi f dikatakan surjektif (surjective) atau pada (onto) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a. Jawab misal 𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 dan 𝐵 = {𝑥, 𝑦, 𝑧} dan fungsi 𝑓: Berikut beberapa contoh relasi fungsi surjektif dalam digaram pemetaan relasi fungsi. Misalnya suatu fungsi himpunan a→b, maka setiap elemen dari b memiliki relasi dengan elemen a tanpa ada satupun elemen di b yang tidak berpasangan.

Source: brainly.co.id

Fungsi f dikatakan injektif jika dan hanya jika untuk setiap x, y a dengan f(x) = f(y) berlaku x = y. Bukan fungsi bijektif, karena unsur fungsi injektif tidak terpenuhi. Sifat fungsi surjektif atau pada atau onto previous activity sifat fungsi : Fungsi surjektif (onto) a b a b pada tidak pada fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan b merupakan bayangan dari satu atau lebih elemen himpunan a. Selanjutnya secara singkat dapat dikatakan bahwa f:a→b adalah fungsi injektif apabila a ≠ b berakibat f (a) ≠.

Source: madematika.net

ℝ → ℝ yang didefinisikan sebagai g(x) = x 2. Fungsi kepada (surjektif) fungsi f : Jawab misal 𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 dan 𝐵 = {𝑥, 𝑦, 𝑧} dan fungsi 𝑓: A → b disebut fungsi surjektif, jika setiap elemen di b mempunyai pasangan di a atau w f = b. Fungsi f dikatakan injektif jika dan hanya jika untuk setiap x, y a dengan f(x) = f(y) berlaku x = y.

This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.

If you find this site serviceableness, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title fungsi surjektif by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.