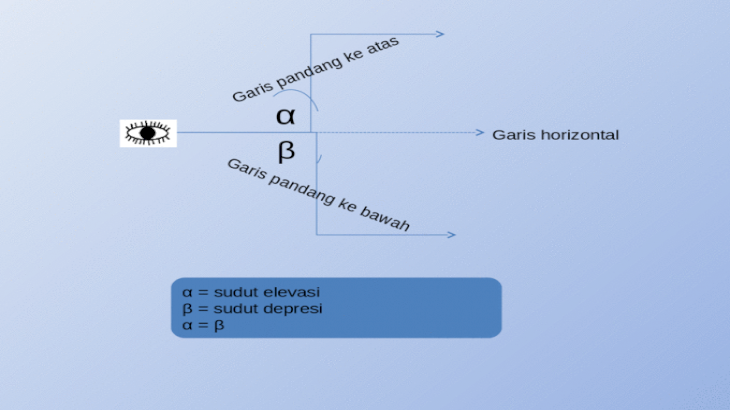
Persamaan Garis Singgung Yang Sejajar. Rumus persamaan garis singgung pada kurva di titik (x 1, y 1) dengan gradien m dimana m = f' (c) sebagai berikut. Jadi, persamaan garis singgung yang melalui titik (2,1) dan menyinggung kurva y=x2−4x+6 adalah y=−2x+5 dan y=2x−3. Gradien dari sebuah persamaan menunjukkan kemiringan garis tersebut. Persamaan garis yang sejajar dengan garis singgung adalah.
Contoh Soal Persamaan Garis Singgung Lingkaran Yang From barucontohsoal.blogspot.com
Gradien garis y = 2x + 9 adalah 2. Karena bentuknya udah ymxc maka tidak perlu diubah. Jadi, persamaan garis singgung yang melalui titik (2,1) dan menyinggung kurva y=x2−4x+6 adalah y=−2x+5 dan y=2x−3. M = f ' (1) = 2 (1) +. Pembahasan garis singgung pada lingkaran dengan pusat (a, b) diketahui gradien m. Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2.
Persamaan garis normal kurva adalah :
Tentukan persamaan garis dengan menggunakan rumusan : Tentukan persamaan garis singgung pada lingkaran tersebut yang sejajar dengan garis y = 2x + 3. Jadi, persamaan garis singgung parabolanya : Jadi, gradien garis singgungnya adalah 20. Y = 12x + 8. Jenis kedua persamaan garis singgung elips yaitu garis singgung elips yang diketahui gradiennya ($m$).
Source: rumushitung.com
Jadi, persamaan garis singgung parabolanya : M = f ' (1) = 2 (1) +. (1, 3) f (x) = x 2 + 2x ⇒ f ' (x) = 2x + 2. Sehingga persamaan garis singgungnya adalah. 1.jika garis singgung tersebut disebut sejajar dgn sebuah garis yang lain,.
Source: belajarsemua.github.io
M = f ' (1) = 2 (1) +. (1, 3) f (x) = x 2 + 2x ⇒ f ' (x) = 2x + 2. Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2. Jika dalam soal disebutkan hubungan antara garis singgung dengan garis yang lain, maka : Persamaan garis yang sejajar dengan garis singgung adalah y 12x 8.
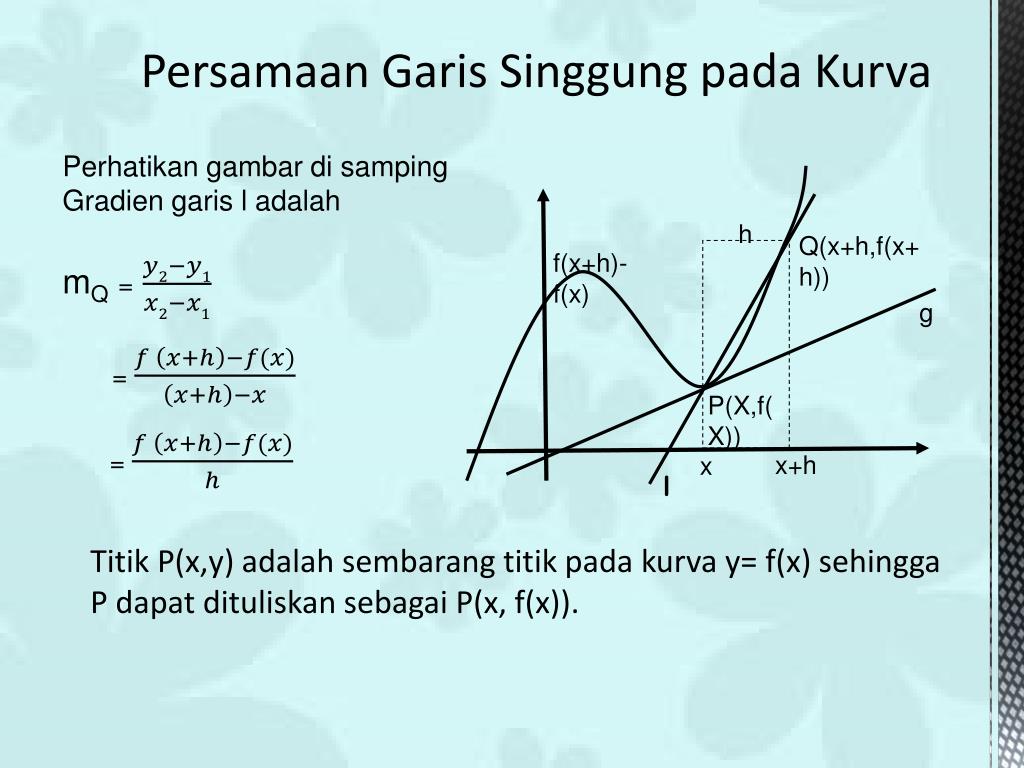Source: belajarsemua.github.io
Persamaan garis yang sejajar dengan garis singgung adalah y 12x 8. Jika dalam soal disebutkan hubungan antara garis singgung dengan garis yang lain, maka : Persamaan garis singgung kurva y = x2 +2x y = x 2 + 2 x dititik (1, 3) ( 1, 3) adalah. Jenis kedua persamaan garis singgung elips yaitu garis singgung elips yang diketahui gradiennya ($m$). M = f ' (1) = 2 (1) +.
Source: brainly.co.id
Menentukan gradien garis singgungnya : Jika dalam soal disebutkan hubungan antara garis singgung dengan garis yang lain, maka : Gradien garis singgung ini sama dengan turunan kurva sehingga. Karena bentuknya udah ymxc maka tidak perlu diubah. M = f ' (1) = 2 (1) +.
Source: barucontohsoal.blogspot.com
Persamaan garis singgung kurva y = x2 +2x y = x 2 + 2 x dititik (1, 3) ( 1, 3) adalah. Karena bentuknya udah ymxc maka tidak perlu diubah. Diketahui persamaan garis singgung lingkaran yang sejajar dengan maka. Jadi, persamaan garis singgung parabolanya : Gradien garis y = 2x + 9 adalah 2.
Source: belajarsemua.github.io
Tentukan persamaan garis yang saling tegak lurus dengan dan melewati titik. $ y = mx \pm \sqrt{a^2m^2 + b^2} $ 2). Persamaan garis singgung kurva y = 0,5x 2 — 7x + 2 yang membentuk sudut 45 o dengan sumbu x positif memotong garis y = 9 — 2x pada koordinat. Berikut bentuk persamaan garis singgung elipsnya : Sejajar dengan atau dapat ditulis dalam bentuk , sehingga garis tersebut mempunyai gradien.
Source: brainly.co.id
Jadi, gradien garis singgungnya adalah 20. Titik singgung antara kurva dan garis (misal : Karena garis singgung yang kita buat sejajar dengan y = 2x + 9 maka gradiennya adalah 2 juga. Jika antara kurva (k) dan garis (g) saling sejajar maka gradiennya sama atau m k = m g. Persamaan garis singgung kurva yang akan admin bahas lagi ini adalah merupakan lanjutan materi sebelumnya yang sudah membahas mengenai mencari persamaan.
Source: brainly.co.id
Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2. Sehingga persamaan garis singgungnya adalah. Jadi, persamaan garis singgung parabolanya : Jenis kedua persamaan garis singgung elips yaitu garis singgung elips yang diketahui gradiennya ($m$). D y d x = 9 x 2 − 12 x + 8 dengan demikian, m = d y d x | x = 2 = 9 ( 2) 2 − 12 ( 2) + 8 = 36 − 24 + 8 = 20.
Source: brainly.co.id
Tentukan persamaan garis normal kurva y=x 2 yang sejajar dengan garis x+4y−5=0! Sejajar dengan atau dapat ditulis dalam bentuk , sehingga garis tersebut mempunyai gradien. Persamaan garis normal kurva adalah : Tentukan persamaan garis yang saling tegak lurus dengan dan melewati titik. Sehingga persamaan garis singgungnya adalah.
Source: brainly.co.id
Tentukan persamaan garis singgung pada lingkaran tersebut yang sejajar dengan garis y = 2x + 3. Gradien garis $ y = 7x + 4 , $ adalah $ m_1 = 7 $ karena garis singgung sejajar dengan garis $ y = 7x + 4 , $ , maka gradiennya sama, sehingga $ m = m_1 = 7 $ artinya gradien garis singgunya adalah 7. Jadi, persamaan garis singgung yang melalui titik (2,1) dan menyinggung kurva y=x2−4x+6 adalah y=−2x+5 dan y=2x−3. (x1, y1)) sudah tentu merupakan titik yang dilalui kurva. Persamaan garis singgung kurva yang akan admin bahas lagi ini adalah merupakan lanjutan materi sebelumnya yang sudah membahas mengenai mencari persamaan.
Source: slideshare.net
D y d x = 9 x 2 − 12 x + 8 dengan demikian, m = d y d x | x = 2 = 9 ( 2) 2 − 12 ( 2) + 8 = 36 − 24 + 8 = 20. Persamaan garis singgung kurva y = x2 +2x y = x 2 + 2 x dititik (1, 3) ( 1, 3) adalah. Jadi, persamaan garis singgung parabolanya : Tentukan persamaan garis singgung pada lingkaran tersebut yang sejajar dengan garis y = 2x + 3. Jika dalam soal disebutkan hubungan antara garis singgung dengan garis yang lain, maka :
Source: brainly.co.id
Persamaan garis singgung kurva yang akan admin bahas lagi ini adalah merupakan lanjutan materi sebelumnya yang sudah membahas mengenai mencari persamaan. Gradien garis singgung ini sama dengan turunan kurva sehingga. Tentukan persamaan garis singgung lingkaran x 2 + y 2 + 6x — 2y — 10 = 0 yang sejajar dengan garis y = 2x + 9. Jenis kedua persamaan garis singgung elips yaitu garis singgung elips yang diketahui gradiennya ($m$). (1, 3) f (x) = x 2 + 2x ⇒ f ' (x) = 2x + 2.
Source: belajarsemua.github.io
D y d x = 9 x 2 − 12 x + 8 dengan demikian, m = d y d x | x = 2 = 9 ( 2) 2 − 12 ( 2) + 8 = 36 − 24 + 8 = 20. Y — 1 = 2x + 6 ± 10. Rumus persamaan garis singgung pada kurva di titik (x 1, y 1) dengan gradien m dimana m = f' (c) sebagai berikut. Persamaan garis normal kurva adalah : 1.jika garis singgung tersebut disebut sejajar dgn sebuah garis yang lain,.
Source: contohsoalitu.blogspot.com
M = f ' (1) = 2 (1) +. M = f ' (1) = 2 (1) +. 2y = 2 2y = 2 y = 2 Gradien dari sebuah persamaan menunjukkan kemiringan garis tersebut. Garis normal adalah garis yang melalui titik singgung kurva dan tegak lurus terhadap garis singgung kurva di titik tersebut.
Source: shareitnow.me
Garis normal adalah garis yang melalui titik singgung kurva dan tegak lurus terhadap garis singgung kurva di titik tersebut. Berikut bentuk persamaan garis singgung elipsnya : Jadi, persamaan garis singgung parabolanya : Bentuk persamaan garis singgung yang akan dibahas di sini adalah garis singgung parabola jika diketahui gradien garis lurus yang menyinggung parabola. Gradien garis $ y = 7x + 4 , $ adalah $ m_1 = 7 $ karena garis singgung sejajar dengan garis $ y = 7x + 4 , $ , maka gradiennya sama, sehingga $ m = m_1 = 7 $ artinya gradien garis singgunya adalah 7.
Source: youtube.com
D y d x = 9 x 2 − 12 x + 8 dengan demikian, m = d y d x | x = 2 = 9 ( 2) 2 − 12 ( 2) + 8 = 36 − 24 + 8 = 20. Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2. Y — 1 = 2x + 6 ± 10. M 2 = m 1 = 12. Gradien garis singgung pada kurva dengan persamaan y = 3 x 3 − 6 x 2 + 8 x + 10 pada x = 2 adalah d y d x | x = 2.
Source: youtube.com
Menentukan gradien garis singgungnya : Persamaan garis singgung kurva yang akan admin bahas lagi ini adalah merupakan lanjutan materi sebelumnya yang sudah membahas mengenai mencari persamaan. Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2. Sejajar dengan atau dapat ditulis dalam bentuk , sehingga garis tersebut mempunyai gradien. Karena sejajar maka gradiennya sama sehingga gradien garis singgung (m 2) adalah.
Source: brainly.co.id
Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2. Jika antara kurva (k) dan garis (g) saling sejajar maka gradiennya sama atau m k = m g. Pembahasan garis singgung pada lingkaran dengan pusat (a, b) diketahui gradien m. Menentukan gradien garis singgungnya : Jenis kedua persamaan garis singgung elips yaitu garis singgung elips yang diketahui gradiennya ($m$).
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title persamaan garis singgung yang sejajar by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
