Rumus Sudut Pusat. Demikian penjelasan materi tentang sudut pusat dan sudut keliling: Ada pun rumus untuk mencari panjang busur ialah. Sudut pusat memiliki besar dua kali sudut kelilingnya karena sama sama menghadap pada satu busur. ∠ acb = 1 2 × ∠ acb ∠ acb = 1 2 × 65° = 32,5° demikian pembahasan mengenai rumus sudut pusat dan sudut keliling lingkaran beserta contoh soalnya, semoga bisa bermanfaat untuk kalian semua.
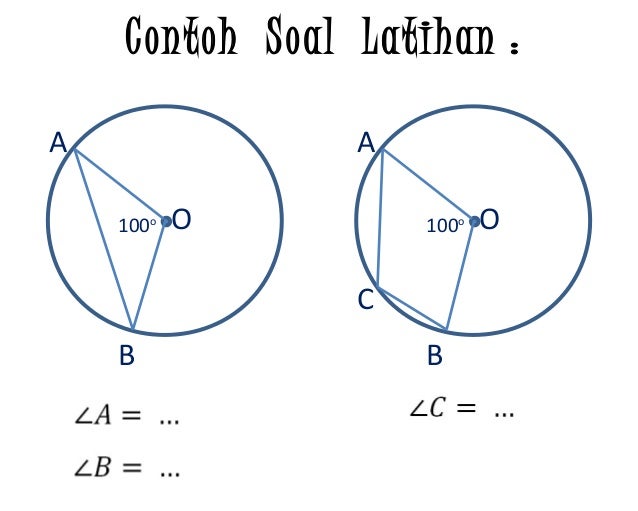Contoh Soal Sudut Pusat Dan Sudut Keliling Berbagai Contoh From berbagaicontoh.com
Panjang ab = (∠ aob/360°) x 2πr. Ada dua tahapan yang harus anda lakukan, yakni: Hubungan antara sudut aob dan sudut acb dengan demikian adalah: Sudut keliling adalah unsur lingkaran selanjutnya yang akan dibahas. Panjang ab = (90°/360°) x 2 x 22/7 x 28 cm. Sehingga 5x 10 2 70 5x 10 140 5x 140 10 5x 150 x 1505 30.
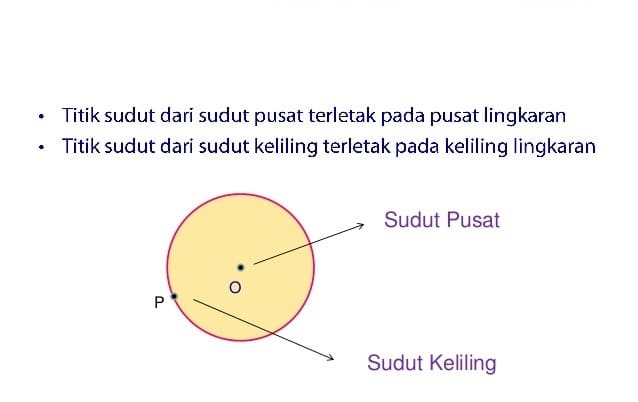
Pada bangun datar lingkaran ada sudut yang bernama sudut pusat dan sudut keliling.
Besar sudut aob (sudut pusat) = 2 x acb (sudut keliling) = 2 x 27°. Lj = (60°/360°) x (22/7) x (7√3 cm)2. Pertidaksamaan nilai mutlak rumus sifat konsep contoh soal from wwwdosenpendidikancoid. Rotasi atau perputaran sebagai salah satu jenis transformasi memiliki aturan dalam mentransformasikan titik atau kurva dengan cara diputar terhadap titik pusat dengan besar sudut tertentu. Untuk menentukan bayangan titik yang di rotasi dengan pusat (0,0) sejauh 90 o dapat dengan menggunakan matriks transformasi , dimana θ = 90 o. Panjang ab = (∠ aob/360°) x 2πr.
Source: slideserve.com
Panjang ab = (∠ aob/360°) x 2πr. Sehingga 5x 10 2 70 5x 10 140 5x 140 10 5x 150 x 1505 30. Untuk itu rumus sudut pusat lingkaran dapat dinyatakan dalam bentuk seperti berikut ini: ∠aob = 2 × ∠acb. Ada pun rumus untuk mencari panjang busur ialah.
Source: pelajaran.co.id
Secara matriks dapat ditulis sebagai: Setelah menjelaskan tentang rumus juring lingkaran di atas. Lj = (1/6) x 462 cm2. Sekarang cari ∆aob dengan cara cepat menghitung luas segitiga sama sisi, yakni: Lj = (α/360°) x πr2.
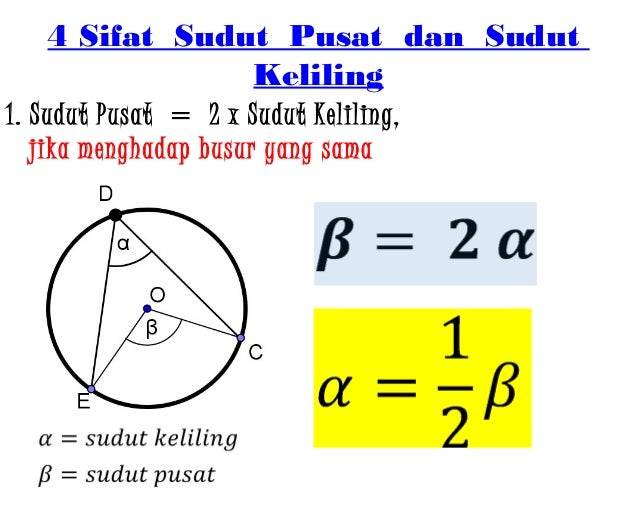Source: senidansastrapopuler.blogspot.com
Rotasi atau perputaran sebagai salah satu jenis transformasi memiliki aturan dalam mentransformasikan titik atau kurva dengan cara diputar terhadap titik pusat dengan besar sudut tertentu. Sudut keliling lingkaran adalah sebuah sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran. Jika besar ∠ aob = 90°, hitunglah. Besar sudut aob (sudut pusat) = 2 x acb (sudut keliling) = 2 x 27°. Sudut a adalah sudut keliling yang menghadap pada busur yang sama dengan sudut pusat sebesar 80º maka besarnya sudut a.
Source: rumadimatematika.blogspot.com
Sebuah lingkaran berpusat di titik o seperti gambar berikut. Untuk itu rumus sudut pusat lingkaran dapat dinyatakan dalam bentuk seperti berikut ini: Besar sudut pusat lingkaran ialah dua kali sudut kelilingnya. Contoh soal luas juring lingkaran. Arah percepatan sentripetal selalu menuju ke pusat lingkaran.
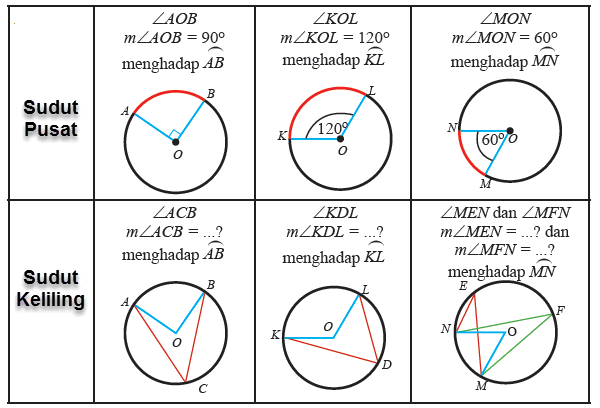Source: mikirbae.com
Sekarang cari ∆aob dengan cara cepat menghitung luas segitiga sama sisi, yakni: Rumus luas kerucut dan contoh soalnya; 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Pengertian, rumus dan cara menghitung sudut pusat dan sudut keliling lingkaran serta contoh soal dan pembahasan super lengkap. Hubungan sudut pusat, panjang busur dan luas juring.
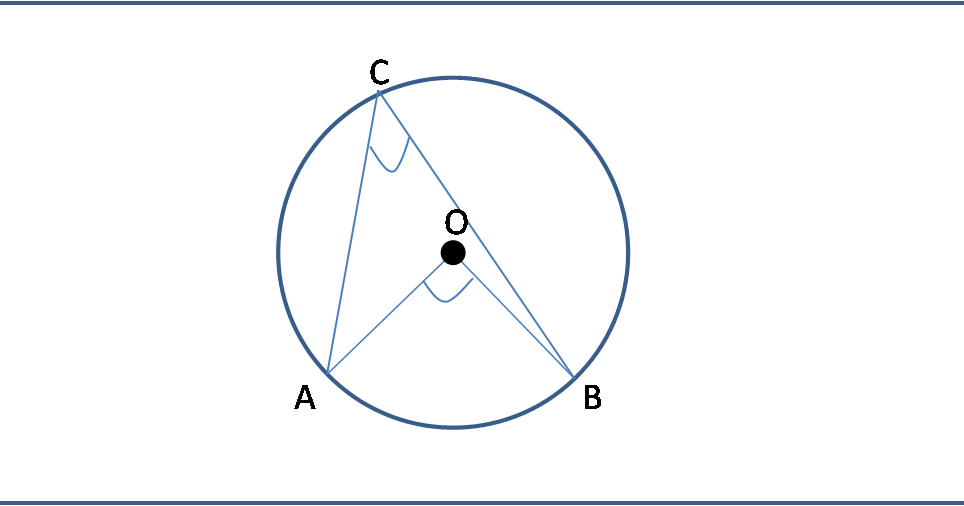Source: barucontohsoal.blogspot.com
Demikian artikel pembahasan tentang pengertian lingkaran, sifat, unsur, rumus, contoh soal lingkaran dan pembahasannya secara lengkap. Sudut pusat = 2 kali. Equation of circle at (0,0) ppt equation of circle; Panjang ab = (∠ aob/360°) x 2πr. Sudut pusat memiliki besar dua kali sudut kelilingnya karena sama sama menghadap pada satu busur.
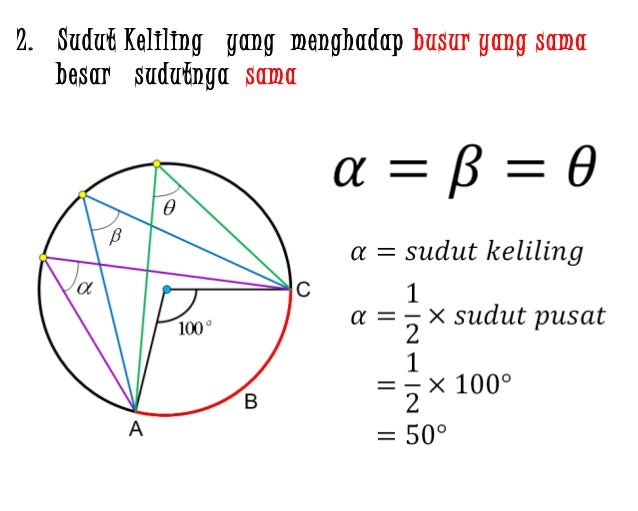Source: berbagaicontoh.com
Rumus luas kerucut dan contoh soalnya; 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Sudut pusat adalah unsur lingkaran selanjutnya yang akan dibahas. Sebuah lingkaran berpusat di titik o seperti gambar berikut. Contoh soal tentang hubungan antara sudut pusat, panjang busur, dan luas juring.
Source: syahrulanam.com
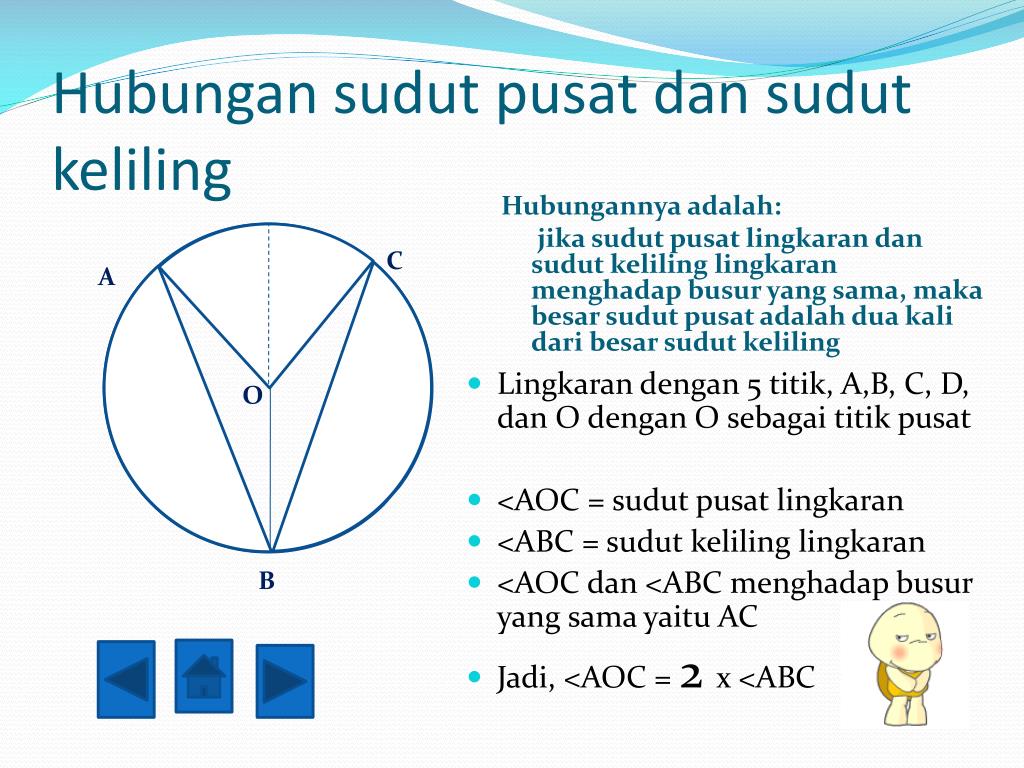
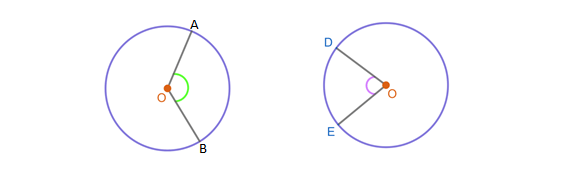
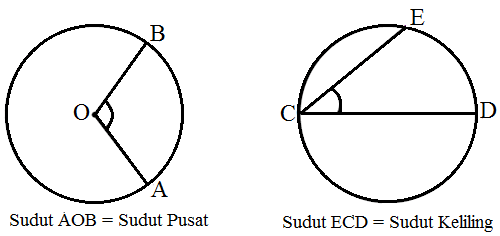
Secara matriks dapat ditulis sebagai: Sudut keliling lingkaran adalah sebuah sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran. Sudut pusat dan sudut keliling lingkaran. Contoh soal tentang hubungan antara sudut pusat, panjang busur, dan luas juring. Sudut aob adalah sudut pusat yang menghadap busur yang sama dengan sudut acb yang merupakan sudut keliling.
Source: rumus.co.id
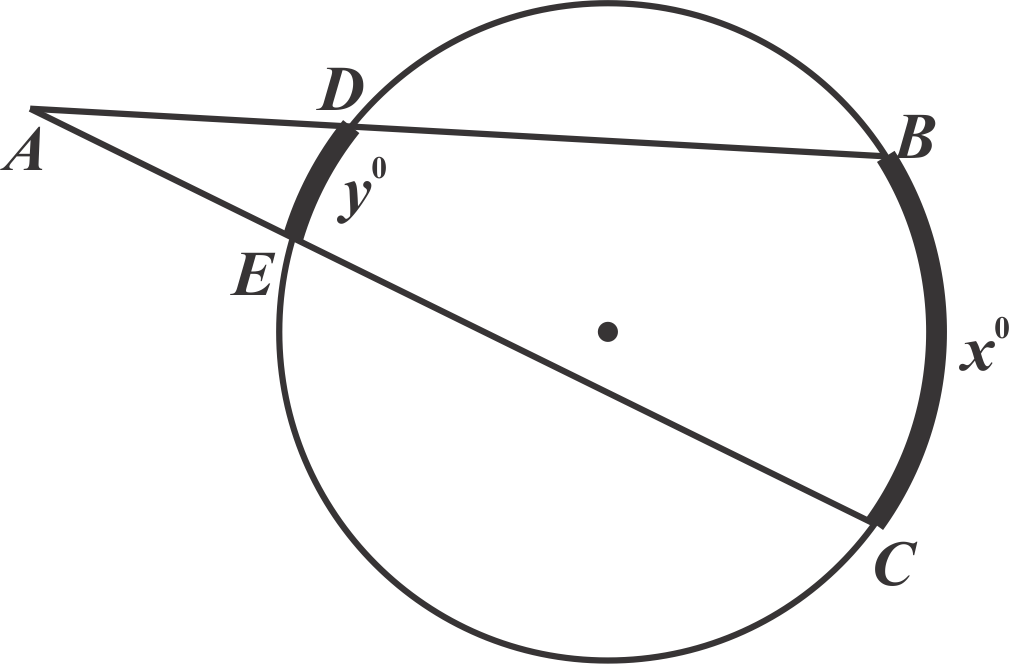
∠aoc = 2 x ∠abc. Pada bangun datar lingkaran ada sudut yang bernama sudut pusat dan sudut keliling. Hubungan sudut pusat, panjang busur dan luas juring. Jika besar ∠ aob = 90°, hitunglah. Lj = (α/360°) x πr2.
Source: berbagaicontoh.com
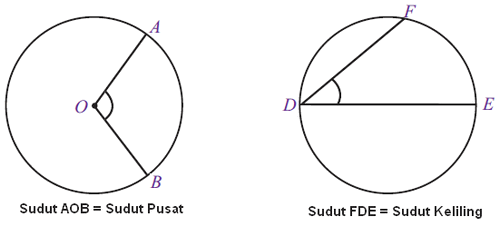
By azzahra rahmah posted on october 9, 2021. Jadi rumus panjang busur lingkaran adalah 28 contoh soal 1. Lj = (60°/360°) x (22/7) x (7√3 cm)2. ∠aob = 2 × ∠acb. Rotasi atau perputaran sebagai salah satu jenis transformasi memiliki aturan dalam mentransformasikan titik atau kurva dengan cara diputar terhadap titik pusat dengan besar sudut tertentu.
Source: mapel-sekolahku.blogspot.com
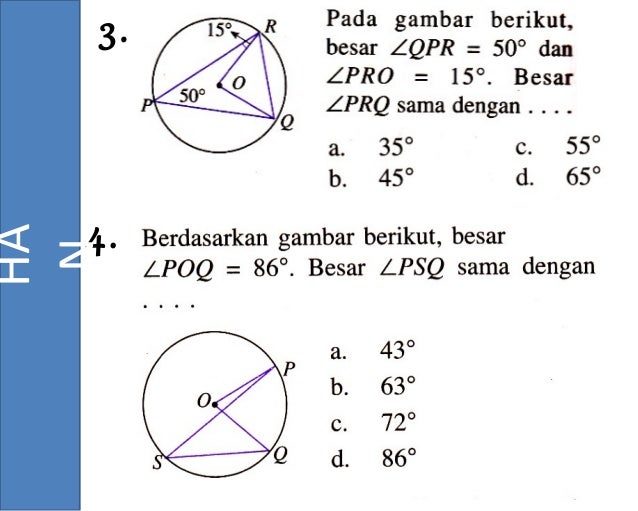
= jarak yang ditempuh (km, m). Contoh soal tentang hubungan antara sudut pusat, panjang busur, dan luas juring. Besar sudut pusat lingkaran ialah dua kali sudut kelilingnya. Lj = (1/6) x 462 cm2. Sudut pusat adalah unsur lingkaran selanjutnya yang akan dibahas.
Source: berbagaicontoh.com
Percepatan sentripetal tidak menambah kecepatan, melainkan hanya untuk mempertahankan benda agar tetap bergerak melingkar. Demikian penjelasan materi tentang sudut pusat dan sudut keliling: Cara menghitung rumus luas segi enam dan contoh soal; Pusat rotasi, merupakan titik sebagai acuan. Ada dua tahapan yang harus anda lakukan, yakni:
Source: antotunggal.com
Sudut pusat dan sudut keliling pembahasan : Lj = (60°/360°) x (22/7) x (7√3 cm)2. Persamaan lingkaran powerpoint + geogebra; Cara menghitung rumus luas segi enam dan contoh soal; By azzahra rahmah posted on october 9, 2021.
Source: pengennaikkelas.blogspot.com
Arah percepatan sentripetal selalu menuju ke pusat lingkaran. Rumus luas kerucut dan contoh soalnya; Ada dua tahapan yang harus anda lakukan, yakni: Hubungan sudut pusat, panjang busur dan luas juring. Untuk menentukan bayangan titik yang di rotasi dengan pusat (0,0) sejauh 90 o dapat dengan menggunakan matriks transformasi , dimana θ = 90 o.
Source: jejakgurudigital.blogspot.com
Rumus luas kerucut dan contoh soalnya; Sudut pusat = 2 kali. Untuk itu rumus sudut pusat lingkarannya dapat menjadi seperti di bawah ini: Untuk menentukan bayangan titik yang di rotasi dengan pusat (0,0) sejauh 90 o dapat dengan menggunakan matriks transformasi , dimana θ = 90 o. Garis lengkung ab disebut busur ab dan daerah arsiran oab disebut juring oab.
Source: rpp.co.id
Selanjutnya saya akan membagikan contoh soal juring lingkaran terkait rumus tersebut. By azzahra rahmah posted on october 9, 2021. Panjang ab = (90°/360°) x 2 x 22/7 x 28 cm. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Contoh soal tentang hubungan antara sudut pusat, panjang busur, dan luas juring.
Source: risalandi.com
Sudut pusat memiliki besar dua kali sudut kelilingnya karena sama sama menghadap pada satu busur. ∠ acb = 1 2 × ∠ acb ∠ acb = 1 2 × 65° = 32,5° demikian pembahasan mengenai rumus sudut pusat dan sudut keliling lingkaran beserta contoh soalnya, semoga bisa bermanfaat untuk kalian semua. Sudut keliling lingkaran adalah sebuah sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran. Hubungan antara sudut aob dan sudut acb dengan demikian adalah: Matriks disebut matriks rotasi dengan pusat di o(0,0) dan sudut putar sebesar θ radian.
Source: brainly.co.id
Sudut pusat adalah unsur lingkaran selanjutnya yang akan dibahas. Untuk itu rumus sudut pusat lingkarannya dapat menjadi seperti di bawah ini: Panjang ab = (90°/360°) x 2 x 22/7 x 28 cm. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Pertidaksamaan nilai mutlak rumus sifat konsep contoh soal from wwwdosenpendidikancoid.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title rumus sudut pusat by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
