Rumus Sudut Pusat Lingkaran. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Menurut sifat di atas maka besarnya ∠qpr = ∠qtr = ∠qsr. Apabila sudut pusat tembereng kurang dari 180 derajat, maka disebut tembereng kecil. Grameds perlu mengetahui berbagai rumus lingkaran agar bisa.
PPT LINGKARAN By RAHIMA PowerPoint Presentation, free From slideserve.com
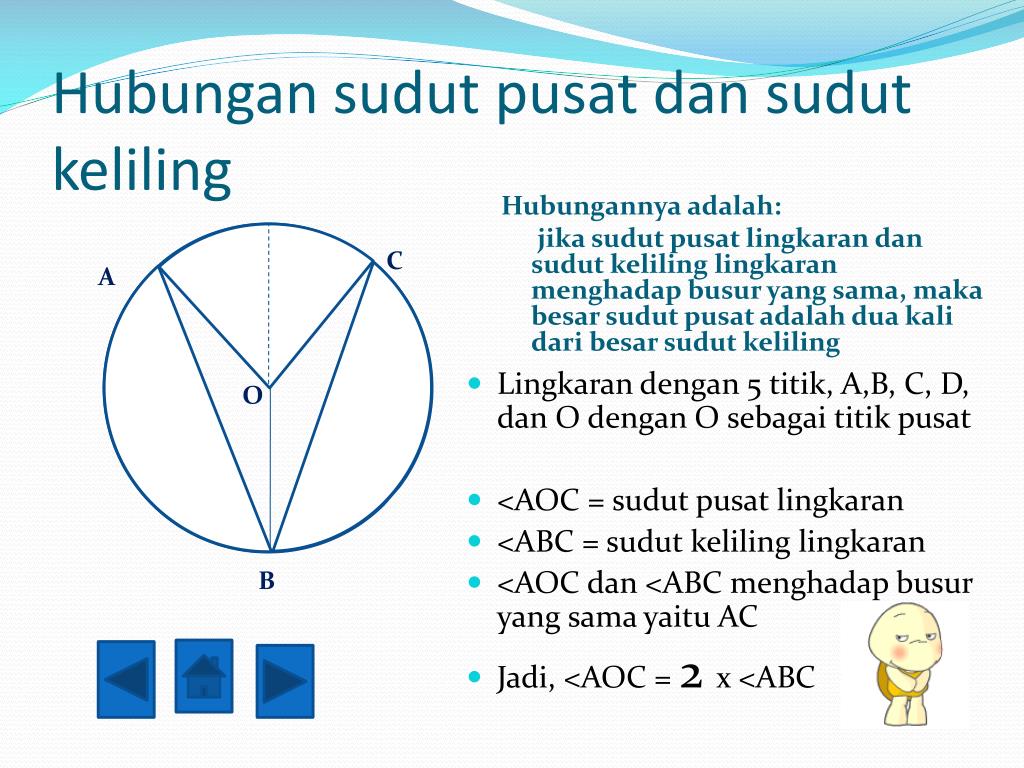
Sudut pusat dan keliling lingkaran. Ada dua tahapan yang harus anda lakukan, yakni: Pada gambar di atas, sudut pusat yang terbentuk antara titik a, o, serta b. Hubungan sudut pusat dan keliling lingkaran. Untuk itu rumus sudut pusat lingkaran dapat dinyatakan dalam bentuk seperti berikut ini: Jika luas juring dan besar sudut pusatnya diketahui, maka kamu bisa menggunakan rumus berikut untuk menghitung luas lingkaran luas juring = alpha/ 3600 x l, dengan alpha adalah besar sudut pusat juring dalam satuan derajat.
Panjang busur ab = sudut pusat / 360º x keliling lingkaran.
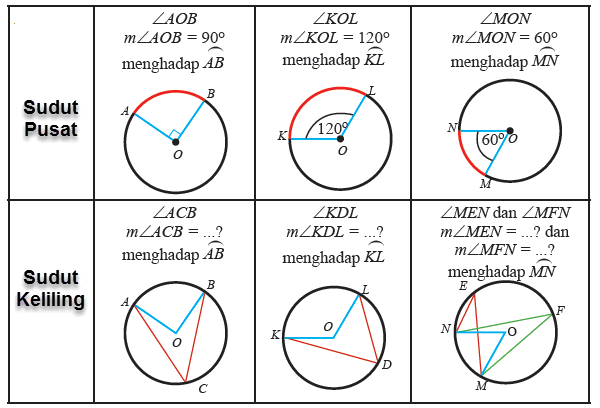
Besar sudut aob (sudut pusat) = 2 x acb (sudut keliling) = 2 x 27°. Panjang busur ab = α/360º x 2 π r. Sudut yang dibentuk oleh perpotongan antara dua buah tali busur di suatu titik pada keliling lingkaran dapat dikatakan sebagai sudut keliling. Cara menghitung rumus luas segi enam dan contoh soal. Selanjutnya saya akan membagikan contoh soal juring lingkaran terkait rumus tersebut. Contoh soal luas juring lingkaran.
Source: youtube.com
Dimana α adalah susut pusat, sudut yang menghadap ke tali busur. Dapatkan pelajaran, soal & rumus sifat sudut pada lingkaran lengkap di wardaya college. Panjang busur ab = sudut pusat / 360º x keliling lingkaran. Sudut yang dibentuk oleh perpotongan antara dua buah tali busur di suatu titik pada keliling lingkaran dapat dikatakan sebagai sudut keliling. Pada bangun datar lingkaran ada sudut yang bernama sudut pusat dan sudut keliling.
Source: brainly.co.id
Demikian penjelasan materi tentang sudut pusat dan sudut keliling: Menurut sifat di atas maka besarnya ∠qpr = ∠qtr = ∠qsr. Panjang busur ab = α/360º x 2 π r. Hal ini disebabkan karena kedua sudut lingkaran ini menghadap pada busur yang sama. Α = sudut pusat π = phi (22/7 atau 3,14) r = jari jari lingkaran.
Source: smatika.blogspot.co.id
Ω = 2 π f. Grameds perlu mengetahui berbagai rumus lingkaran agar bisa. Apabila sudut pusat tembereng kurang dari 180 derajat, maka disebut tembereng kecil. Hitunglah luas tembereng (luas diarsir)! Sudut pusat adalah sudut yang dibentuk oleh titik pusat dengan dua titik yang terletak pada lingkaran, sedangkan sudut keliling adalah sudut yang dibentuk oleh tiga.
Source: mikirbae.com
Di bawah ini terdapat hubungan pada kedua sudut lingkaran yaitu sebagai berikut: Semakin besar sebuah sudut, maka semakin panjang sebuah busur dan semakin luas sebuah juring. Lj = (α/360°) x πr2. Ada pun rumus untuk mencari panjang busur ialah. ∠aoc = 2 x ∠abc.
Source: slideserve.com
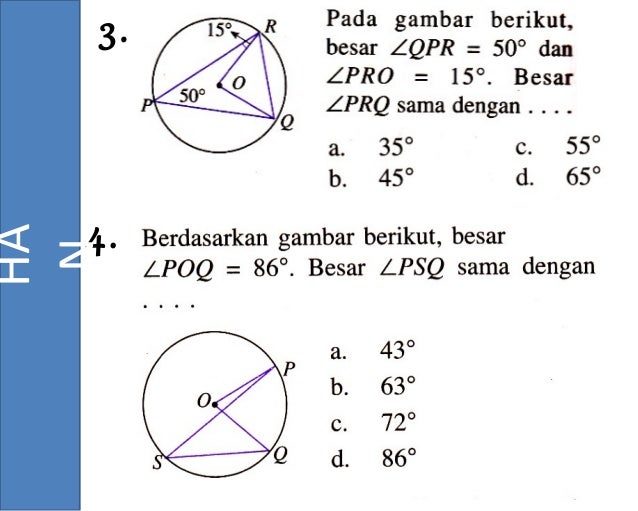
Luas juring aob = sudut pusat / 360º x luas lingkaran. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Sudut prq besarnya adalah 90 derajat. Contoh soal sudut pusat lingkaran dan sudut keliling lengkap. ∠aoc = 2 x ∠abc.
Source: kelaspintar.id
Pengertian sudut pusat dan sudut keliling lingkaran pengertian, rumus dan cara menghitung sudut pusat dan sudut keliling lingkaran serta contoh soal dan pembahasan super lengkap. Sudut pusat dan keliling lingkaran. Jika luas juring dan besar sudut pusatnya diketahui, maka kamu bisa menggunakan rumus berikut untuk menghitung luas lingkaran luas juring = alpha/ 3600 x l, dengan alpha adalah besar sudut pusat juring dalam satuan derajat. Demikian penjelasan materi tentang sudut pusat dan sudut keliling: ∠aoc = 2 x ∠abc.
Source: bagicontohsoal.blogspot.com
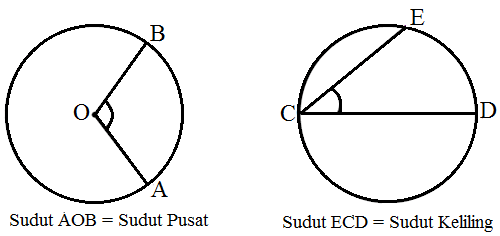
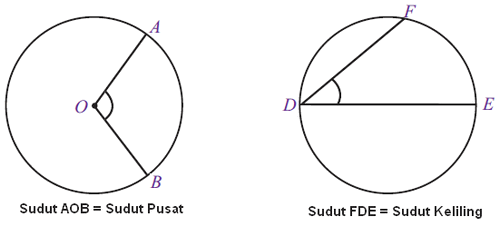
Untuk itu rumus sudut pusat lingkaran dapat dinyatakan dalam bentuk seperti berikut ini: ∠aob = ∝ adalah sudut pusat lingkaran. Oke sekarang kita akan membahas rumus rumus yang ada pada gerak melingkar dan turunannya. Pada bangun datar lingkaran ada sudut yang bernama sudut pusat dan sudut keliling. ∠aoc = 2 x ∠abc.
Source: brainly.co.id
Dimana α adalah susut pusat, sudut yang menghadap ke tali busur. Belajar sifat sudut pada lingkaran dengan video dan kuis interaktif. Apabila lebih dari 180 derajat, maka disebut tembereng besar. Setelah menjelaskan tentang rumus juring lingkaran di atas. ∠aoc = 2 x ∠abc.
Source: rumadimatematika.blogspot.com
Menurut sifat di atas maka besarnya ∠qpr = ∠qtr = ∠qsr. Luas juring aob = α/360º x π r 2. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Α = sudut pusat π = phi (22/7 atau 3,14) r = jari jari lingkaran. Hal ini disebabkan karena kedua sudut lingkaran ini menghadap pada busur yang sama.
Source: antotunggal.com
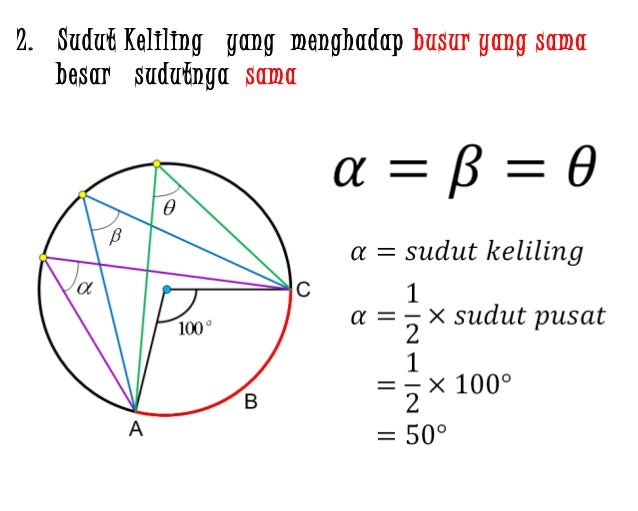
Π = 22/7 atau 3. Sudut keliling yang menghadap busur yang sama akan memiliki besar sudut yang sama pula. ∠aob = ∝ adalah sudut pusat lingkaran. Sudut keliling lingkaran adalah sebuah sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat).
Source: rumus.co.id
Contoh soal luas juring lingkaran. Semakin besar sebuah sudut, maka semakin panjang sebuah busur dan semakin luas sebuah juring. Besar sudut pusat lingkaran ialah dua kali sudut kelilingnya. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Dalam materi lingkaran tersebut tentunya terdapat beberapa hal yang di bahas seperti pengertian sudut pusat lingkaran, pengertian sudut keliling lingkaran, contoh soal pada materi sudut pusat lingkaran dan contoh soal pada materi.
Source: berbagaicontoh.com
Jika luas juring dan besar sudut pusatnya diketahui, maka kamu bisa menggunakan rumus berikut untuk menghitung luas lingkaran luas juring = alpha/ 3600 x l, dengan alpha adalah besar sudut pusat juring dalam satuan derajat. Pengertian sudut pusat dan sudut keliling lingkaran pengertian, rumus dan cara menghitung sudut pusat dan sudut keliling lingkaran serta contoh soal dan pembahasan super lengkap. Panjang busur ab = α/360º x 2 π r. ∠aob = ∝ adalah sudut pusat lingkaran. Ω = 2 π / t.
Source: youtube.com
∠aoc = 2 x ∠abc. Sudut yang dibentuk oleh perpotongan antara dua buah tali busur di suatu titik pada keliling lingkaran dapat dikatakan sebagai sudut keliling. Besar sudut pusat lingkaran ialah dua kali sudut kelilingnya. 1) membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Dimana α adalah susut pusat, sudut yang menghadap ke tali busur.
Source: antotunggal.com
∠aoc = 2 x ∠abc. Ω = 2 π / t. Lj = (60°/360°) x (22/7) x (7√3 cm)2. Luas juring aob = sudut pusat / 360º x luas lingkaran. Α = sudut pusat π = phi (22/7 atau 3,14) r = jari jari lingkaran.
Source: bagicontohsoal.blogspot.com
Sudut prq besarnya adalah 90 derajat. Semakin besar sebuah sudut, maka semakin panjang sebuah busur dan semakin luas sebuah juring. Dimana α adalah susut pusat, sudut yang menghadap ke tali busur. Contoh soal luas juring lingkaran. Sudut pusat adalah sudut yang dibentuk oleh titik pusat dengan dua titik yang terletak pada lingkaran, sedangkan sudut keliling adalah sudut yang dibentuk oleh tiga.
Source: berbagaicontoh.com
Jika luas juring dan besar sudut pusatnya diketahui, maka kamu bisa menggunakan rumus berikut untuk menghitung luas lingkaran luas juring = alpha/ 3600 x l, dengan alpha adalah besar sudut pusat juring dalam satuan derajat. Sudut pusat dan keliling lingkaran. Sudut prq besarnya adalah 90 derajat. Ω = 2 π f. Ω = v / r.
Source: rumushitung.com
Semakin besar sebuah sudut, maka semakin panjang sebuah busur dan semakin luas sebuah juring. Selanjutnya saya akan membagikan contoh soal juring lingkaran terkait rumus tersebut. Sudut prq besarnya adalah 90 derajat. Ω = v / r. Luas juring aob = sudut pusat / 360º x luas lingkaran.
Source: pelajaran.co.id
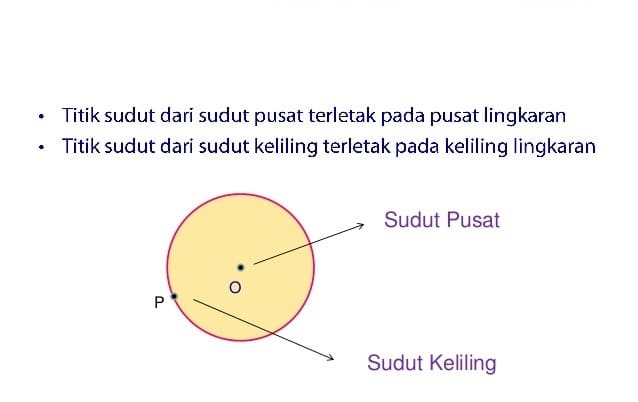
- membagi sudut satu lingkaran penuh (360°) dengan sudut pusat 2) membagi keliling lingkaran dengan hasil no 1 (sudut satu lingkaran penuh (360°) dengan sudut pusat). Menurut sifat di atas maka besarnya ∠qpr = ∠qtr = ∠qsr. Ω = 2 π f. Pada bangun datar lingkaran ada sudut yang bernama sudut pusat dan sudut keliling. Besar sudut pusat lingkaran ialah dua kali sudut kelilingnya.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site helpful, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title rumus sudut pusat lingkaran by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
